感觉最近做题量少了点，写并查集的时候发现find函数有点生疏了。所以这里写个详解，也算是自己的一个复习吧。

并查集就是一棵很奇怪的树。

看看度娘的解释吧：https://baike.baidu.com/item/%E5%B9%B6%E6%9F%A5%E9%9B%86/9388442?fr=aladdin

奇怪在哪里呢？

它奇怪在它只能长这样：

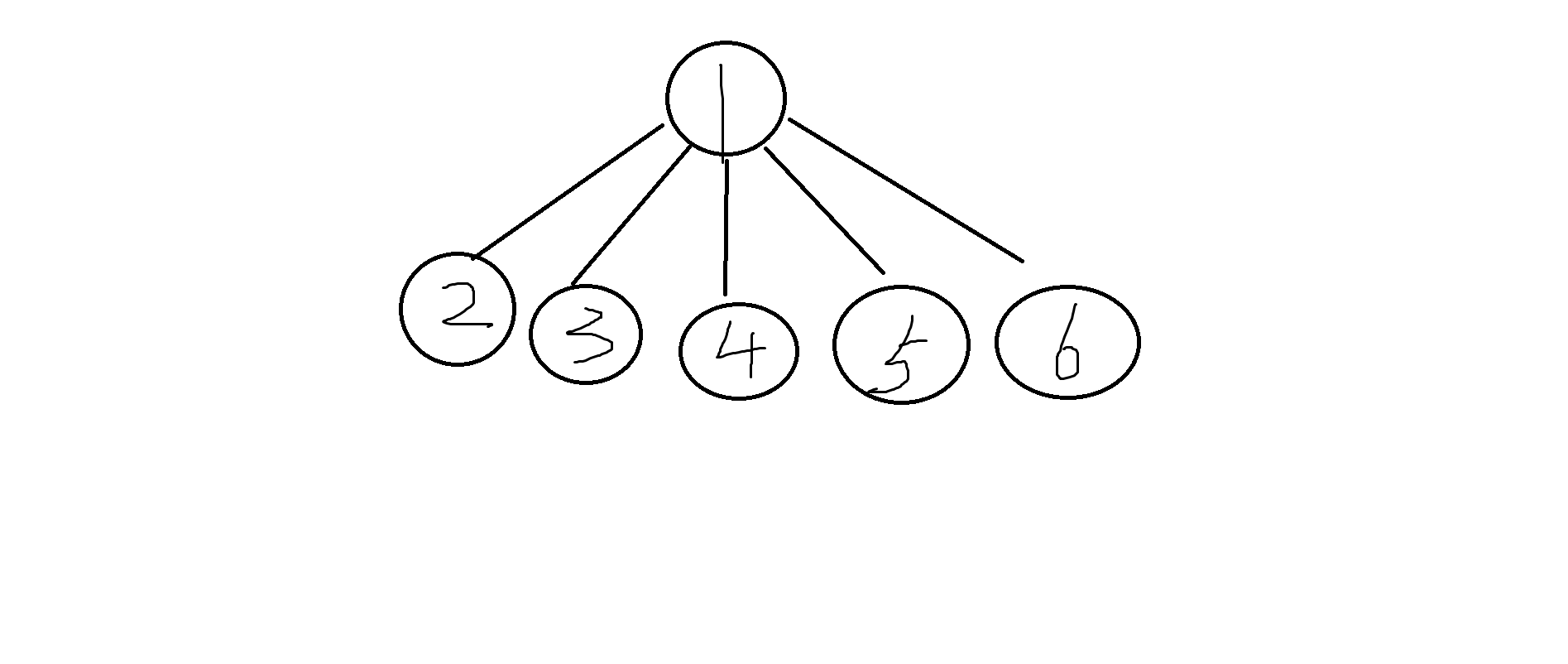
图很简陋勿喷

从这个图中我们应该能很容易地发现这棵树每个节点的父亲就是自己的祖先（根节点除外）。

那么这有什么好处呢？？？

我们也应该很容易就能想到，，，

对啊，只需要保存在这棵树上每一个节点的祖先不就可以保存下这一棵树了嘛。。

所以用并查集的好处就出来了：时间、空间复杂度和编程难度都大大降低。

好了把这些虚无的东西讲完了，我们来看看到底怎么来维护并查集。

首先，你得把这棵树给存下，所以先开一个数组叫pre[]，它就是来存放每个节点的祖先的。

int pre[maxN];

然后你当然要先初始化一下

void init(){    for(int i = 1; i <= n; i ++)        pre[i] = i;  }

这段代码也应该很容易理解，因为每个节点最开始的节点都是自己。

然后我们马上要写维护并查集的代码的核心部分：查询函数和合并函数了。

 先写查询函数吧。查询函数就是要查询一个节点的祖先节点。

大家可以先自己思考思考大概的代码怎么写，然后再往下看。

————————————————————我是分割线————————————————————

先上代码，然后再来解释吧。

int find(int x){    if(x != pre[x]) pre[x] = find(pre[x]);    return pre[x];  }

如果x的祖先不是x，那么就要不断地用递归的形式来查找x的祖先。

最后返回pre[x]即可。

因为这段代码是用递归实现的，所以可能理解上要困难一些，多画几个图，自己拿笔来试试，可能理解地就会更加透彻一点。

当然find函数同样也可以不用递归来实现，大家可以去看看别的大佬们的博客。因为非递归形式的代码比递归形式的要长一些，所以这里就不介绍了。

至于时间复杂度，一般情况下递归形式的find函数要比非递归形式的快一点点。但是嘛，递归。。。。。。毒瘤出题人已经准备卡你了

请先把find函数弄明白再往下看，自己一定要理解透彻！毕竟并查集是NOIP难度的数据结构，提高组有时也会考到（NOIPD2T1）。

————————————————————我是分割线，我又回来了————————————————————

好的，查询函数我们已经讲完了，我们下面要开始讲合并函数了。

合并函数要干的事情就是把两个集合给合并到一块去。

傻傻听不懂？良心的博主已经准备好了粗糙的图，就等你来看啦！

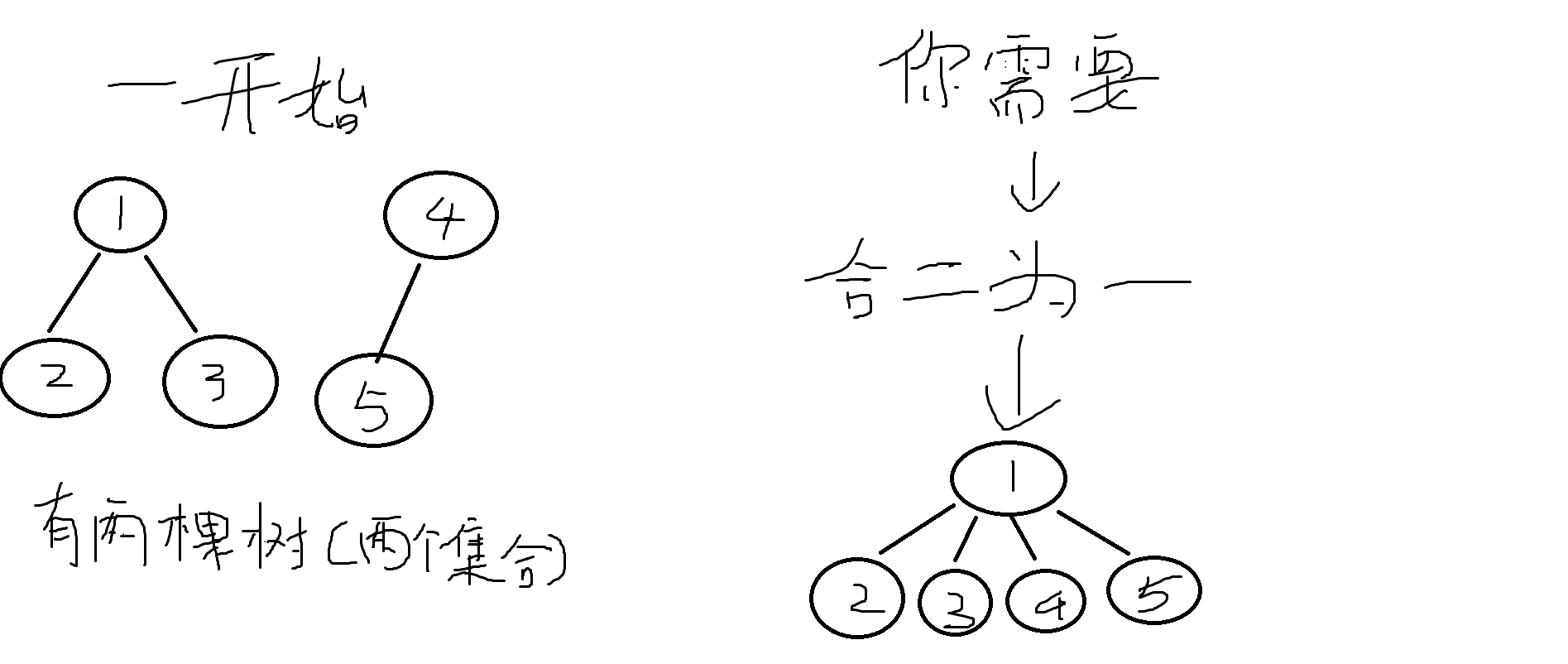
而join函数就是要做上面这张图做的事情。

很显然，你想合并两颗树先要做什么呢？

肯定先要把这两棵树的祖先找到啊，找到这两棵树的祖先节点了，然后再随便把一个祖先的所有子孙（包括这个祖先）全部给另外一个祖先，然后不就OK了？

先理解下上面这句话，然后往下看代码吧！

 

 

 

void join(int x, int y){    int fx = find(x), fy = find(y);    if(fx != fy)        pre[fx] = fy;  }

先找到x和y的祖先，如果x和y的祖先不相同就将两家人合并起来（2333）。